Draw Properties of Triangle Using the Python Matplotlib Module

Draw Properties of Triangle Using the Python Matplotlib Module

In this blog, we will draw properties of triangle using matplotlib module. In this way, students can easily visualize the properties of triangles and learn faster.

Import matplotlib.pyplot module

In [1]:
import matplotlib.pyplot as plt

Plot a point at (0,0)

In [2]:
plt.plot(0, 0, color = 'red', marker = 'o', markersize = 10)
plt.show()

Plot two more points and connect all three points

First point(0, 0) shift to left 5. Then create two more points and connect all three points so that it will become a triangle.

In [3]:
plt.plot(-5, 0, marker = 'o', markersize = 10)
plt.plot(10, 0, marker = 'o', markersize = 10)
plt.plot(0, 8, marker = 'o', markersize = 10)

#connecting all three points to make triangle
plt.plot( 
    (-5, 10, 0, -5),   
    (0, 0, 8, 0)    
)

plt.show()

Write Name of the points like 'A', 'B', 'C'.

In [4]:
plt.plot(-5, 0, marker = 'o', markersize = 10)
plt.plot(10, 0, marker = 'o', markersize = 10)
plt.plot(0, 8, marker = 'o', markersize = 10)

# connecting all three points to make triangle
plt.plot( 
    (-5, 10, 0, -5),   
    (0, 0, 8, 0)    
)

# name of the points 
plt.text(-5.9, 0, 'A')
plt.text(10.4, 0, 'B')
plt.text(0, 8.3, 'C')

plt.show()

Set the x-limit and y-limit

In [5]:
plt.plot(-5, 0, marker = 'o', markersize = 10)
plt.plot(10, 0, marker = 'o', markersize = 10)
plt.plot(0, 8, marker = 'o', markersize = 10)

# connecting all three points to make triangle
plt.plot( 
    (-5, 10, 0, -5),   
    (0, 0, 8, 0)    
)

# name of the points 
plt.text(-5.9, 0, 'A')
plt.text(10.4, 0, 'B')
plt.text(0, 8.3, 'C')

#set the xlim and ylim
plt.xlim(-10,15)
plt.ylim(-2,10)

plt.show()

Change x and y coordinates in variables

We will change all x and y coordnates in variables.

In [6]:
x1, y1 = -5, 0
x2, y2 = 10, 0
x3, y3 = 0, 8

plt.plot(x1, y1, marker = 'o', markersize = 10)
plt.plot(x2, y2, marker = 'o', markersize = 10)
plt.plot(x3, y3, marker = 'o', markersize = 10)

# connecting all three points to make triangle
plt.plot( 
    (x1, x2, x3, x1),   
    (y1, y2, y3, y1)    
)

# name of the points 
plt.text(x1 - 0.9, y1, 'A')
plt.text(x2 + 0.4, y2, 'B')
plt.text(x3, y3 + 0.3, 'C')

#set the xlim and ylim
plt.xlim(-10,15)
plt.ylim(-2,10)

plt.show()

Find the mid point of AB and draw median

A median of a triangle is a straight line through a vertex and the midpoint of the opposite side, and divides the triangle into two equal areas.

Draw the mid point of AB

In [7]:
x1, y1 = -5, 0
x2, y2 = 10, 0
x3, y3 = 0, 8

plt.plot(x1, y1, marker = 'o', markersize = 10)
plt.plot(x2, y2, marker = 'o', markersize = 10)
plt.plot(x3, y3, marker = 'o', markersize = 10)

# connecting all three points to make triangle
plt.plot( 
    (x1, x2, x3, x1),   
    (y1, y2, y3, y1)    
)

# name of the points 
plt.text(x1 - 0.9, y1, 'A')
plt.text(x2 + 0.4, y2, 'B')
plt.text(x3, y3 + 0.3, 'C')


#mid point of AB
m1x = (x1 + x2)/2
m1y = (y1 + y2)/2
plt.plot(m1x, m1y, marker = 'o', color = 'red')

plt.text(m1x, m1y-.5, 'M1')


#set the xlim and ylim
plt.xlim(-10,15)
plt.ylim(-2,10)

plt.show()

Draw the median

In [8]:
x1, y1 = -5, 0
x2, y2 = 10, 0
x3, y3 = 0, 8

plt.plot(x1, y1, marker = 'o', markersize = 10)
plt.plot(x2, y2, marker = 'o', markersize = 10)
plt.plot(x3, y3, marker = 'o', markersize = 10)

# connecting all three points to make triangle
plt.plot( 
    (x1, x2, x3, x1),   
    (y1, y2, y3, y1)    
)

# name of the points 
plt.text(x1 - 0.9, y1, 'A')
plt.text(x2 + 0.4, y2, 'B')
plt.text(x3, y3 + 0.3, 'C')


#mid point of AB
m1x = (x1 + x2)/2
m1y = (y1 + y2)/2
plt.plot(m1x, m1y, marker = 'o', color = 'red')

plt.text(m1x, m1y-.5, 'M1')

#median 1
plt.plot(
    (x3, m1x ),     
    (y3, m1y )
)

#set the xlim and ylim
plt.xlim(-10,15)
plt.ylim(-2,10)

plt.show()

Find the mid point of AC and median

In [9]:
x1, y1 = -5, 0
x2, y2 = 10, 0
x3, y3 = 0, 8

plt.plot(x1, y1, marker = 'o', markersize = 10)
plt.plot(x2, y2, marker = 'o', markersize = 10)
plt.plot(x3, y3, marker = 'o', markersize = 10)

# connecting all three points to make triangle
plt.plot( 
    (x1, x2, x3, x1),   
    (y1, y2, y3, y1)    
)

# name of the points 
plt.text(x1 - 0.9, y1, 'A')
plt.text(x2 + 0.4, y2, 'B')
plt.text(x3, y3 + 0.3, 'C')


#middle point of AB
m1x = (x1 + x2)/2
m1y = (y1 + y2)/2
plt.plot(m1x, m1y, marker = 'o', color = 'red')

plt.text(m1x, m1y-.5, 'M1')

#median from C to AB
plt.plot(
    (x3, m1x ),     
    (y3, m1y )
)

#middle point of AC
m2x = (x1 + x3) / 2
m2y = (y1 + y3) / 2

plt.plot(m2x, m2y, marker = 'o', color = 'black')
plt.text(m2x - 1.5, m2y, 'M2')

#middle point of B to AC
plt.plot(
    (x2, m2x),
    (y2, m2y)
)

#set the xlim and ylim
plt.xlim(-10,15)
plt.ylim(-2,10)

plt.show()

Find the mid point of BC and median

In [10]:
x1, y1 = -5, 0
x2, y2 = 10, 0
x3, y3 = 0, 8

plt.plot(x1, y1, marker = 'o', markersize = 10)
plt.plot(x2, y2, marker = 'o', markersize = 10)
plt.plot(x3, y3, marker = 'o', markersize = 10)

# connecting all three points to make triangle
plt.plot( 
    (x1, x2, x3, x1),   
    (y1, y2, y3, y1)    
)

# name of the points 
plt.text(x1 - 0.9, y1, 'A')
plt.text(x2 + 0.4, y2, 'B')
plt.text(x3, y3 + 0.3, 'C')


#middle point of AB
m1x = (x1 + x2)/2
m1y = (y1 + y2)/2
plt.plot(m1x, m1y, marker = 'o', color = 'red')

plt.text(m1x, m1y-.5, 'M1')

#median from C to AB
plt.plot(
    (x3, m1x ),     
    (y3, m1y )
)

#middle point of AC
m2x = (x1 + x3) / 2
m2y = (y1 + y3) / 2

plt.plot(m2x, m2y, marker = 'o', color = 'black')
plt.text(m2x - 1.5, m2y, 'M2')

#middle point of B to AC
plt.plot(
    (x2, m2x),
    (y2, m2y)
)

#median from A to BC
m3x = (x2 + x3)/2
m3y = (y2 + y3)/2
plt.plot(m3x , m3y, marker= 'o' , color ='violet')
plt.text(m3x , m3y , 'M3')

plt.plot( 
    (x1, m3x), 
    (y1, m3y)
)

#set the xlim and ylim
plt.xlim(-10,15)
plt.ylim(-2,10)

plt.show()

Plot Centroid

The three medians intersect at a single point, that point is the triangle's centroid.

In [11]:
x1, y1 = -5, 0
x2, y2 = 10, 0
x3, y3 = 0, 8

plt.plot(x1, y1, marker = 'o', markersize = 10)
plt.plot(x2, y2, marker = 'o', markersize = 10)
plt.plot(x3, y3, marker = 'o', markersize = 10)

# connecting all three points to make triangle
plt.plot( 
    (x1, x2, x3, x1),   
    (y1, y2, y3, y1)    
)

# name of the points 
plt.text(x1 - 0.9, y1, 'A')
plt.text(x2 + 0.4, y2, 'B')
plt.text(x3, y3 + 0.3, 'C')


#middle point of AB
m1x = (x1 + x2)/2
m1y = (y1 + y2)/2
plt.plot(m1x, m1y, marker = 'o', color = 'red')

plt.text(m1x, m1y-.5, 'M1')

#median from C to AB
plt.plot(
    (x3, m1x ),     
    (y3, m1y )
)

#middle point of AC
m2x = (x1 + x3) / 2
m2y = (y1 + y3) / 2

plt.plot(m2x, m2y, marker = 'o', color = 'black')
plt.text(m2x - 1.5, m2y, 'M2')

#middle point of B to AC
plt.plot(
    (x2, m2x),
    (y2, m2y)
)

#median from A to BC
m3x = (x2 + x3)/2
m3y = (y2 + y3)/2
plt.plot(m3x , m3y, marker= 'o' , color ='violet')
plt.text(m3x , m3y , 'M3')

plt.plot( 
    (x1, m3x), 
    (y1, m3y)
)

#centroid
mx = (x1 + x2 + x3)/3
my = (y1 + y2 + y3)/3
plt.plot( mx, my, marker = 'o',  color = 'orange')

plt.text(mx, my+.5 , 'M')

#set the xlim and ylim
plt.xlim(-10,15)
plt.ylim(-2,10)

plt.show()

Add points coordinates

In [12]:
x1, y1 = -5, 0
x2, y2 = 10, 0
x3, y3 = 0, 8

plt.plot(x1, y1, marker = 'o', markersize = 10)
plt.plot(x2, y2, marker = 'o', markersize = 10)
plt.plot(x3, y3, marker = 'o', markersize = 10)

# connecting all three points to make triangle
plt.plot( 
    (x1, x2, x3, x1),   
    (y1, y2, y3, y1)    
)

# name of the points 
plt.text(x1 - 2.3, y1 + 0.3, f'A({x1}, {y1})')
plt.text(x2 + 0.4, y2, f'B({x2}, {y2})')
plt.text(x3, y3 + 0.3, f'C({x3}, {y3})')


#middle point of AB
m1x = (x1 + x2)/2
m1y = (y1 + y2)/2
plt.plot(m1x, m1y, marker = 'o', color = 'red')

plt.text(m1x, m1y-.5, 'M1')

#median from C to AB
plt.plot(
    (x3, m1x ),     
    (y3, m1y )
)

#middle point of AC
m2x = (x1 + x3) / 2
m2y = (y1 + y3) / 2

plt.plot(m2x, m2y, marker = 'o', color = 'black')
plt.text(m2x - 1.5, m2y, 'M2')

#middle point of B to AC
plt.plot(
    (x2, m2x),
    (y2, m2y)
)

#median from A to BC
m3x = (x2 + x3)/2
m3y = (y2 + y3)/2
plt.plot(m3x , m3y, marker= 'o' , color ='violet')
plt.text(m3x , m3y , 'M3')

plt.plot( 
    (x1, m3x), 
    (y1, m3y)
)

#centeroid
mx = (x1 + x2 + x3)/3
my = (y1 + y2 + y3)/3
plt.plot( mx, my, marker = 'o',  color = 'orange')

plt.text(mx, my+.5 , 'M')

#set the xlim and ylim
plt.xlim(-10,15)
plt.ylim(-2,10)

plt.show()

Find the distance between AB, BC and CA

Now we will find the distance between AB, BC, CA. The distance between points (x1, y1) and (x2, y2) in the plane is given by:

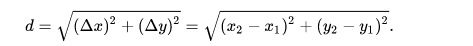
In [13]:
x1, y1 = -5, 0
x2, y2 = 10, 0
x3, y3 = 0, 8

plt.plot(x1, y1, marker = 'o', markersize = 10)
plt.plot(x2, y2, marker = 'o', markersize = 10)
plt.plot(x3, y3, marker = 'o', markersize = 10)

# connecting all three points to make triangle
plt.plot( 
    (x1, x2, x3, x1),   
    (y1, y2, y3, y1)    
)

# name of the points 
plt.text(x1 - 2.3, y1 + 0.3, f'A({x1}, {y1})')
plt.text(x2 + 0.4, y2, f'B({x2}, {y2})')
plt.text(x3, y3 + 0.3, f'C({x3}, {y3})')


# AB distance 
ABx = (x1 + x2) / 2
ABy = (y1 + y2) / 2
plt.text(ABx, ABy - 0.6, f'AB({x2 - x1}, {y2 - y1})')

# BC distance
BCx = (x2 + x3) / 2
BCy = (y2 + y3) / 2
plt.text(BCx - 2, BCy + 0.4, f'BC({x3 - x2}, {y3 - y2})', rotation = -50)

# CA distance
CAx = (x3 + x1) / 2
CAy = (y3 + y1) / 2
plt.text(CAx - 1.3, CAy, f'AC({x1 - x3}, {y1 - y3})', rotation = 65)

#set the xlim and ylim
plt.xlim(-10,15)
plt.ylim(-2,10)

plt.show()
In [14]:
x1, y1 = -5, 0
x2, y2 = 10, 0
x3, y3 = 0, 8

plt.plot(x1, y1, marker = 'o', markersize = 10)
plt.plot(x2, y2, marker = 'o', markersize = 10)
plt.plot(x3, y3, marker = 'o', markersize = 10)

# connecting all three points to make triangle
plt.plot( 
    (x1, x2, x3, x1),   
    (y1, y2, y3, y1)    
)

# name of the points 
plt.text(x1 - 2.3, y1 + 0.3, f'A({x1}, {y1})')
plt.text(x2 + 0.4, y2, f'B({x2}, {y2})')
plt.text(x3, y3 + 0.3, f'C({x3}, {y3})')


# AB distance 
ABsqr = (x2 - x1) ** 2 + (y2 - y1) ** 2
print(ABsqr)

ABx = (x1 + x2) / 2
ABy = (y1 + y2) / 2
plt.text(ABx, ABy - 0.6, f'AB({x2 - x1}, {y2 - y1})')

# BC distance
BCsqr = (x3 - x2) ** 2 + (y3 - y2) ** 2
print(BCsqr)

BCx = (x2 + x3) / 2
BCy = (y2 + y3) / 2
plt.text(BCx - 2, BCy + 0.4, f'BC({x3 - x2}, {y3 - y2})', rotation = -50)

# CA distance
CAsqr = (x1 - x3) ** 2 + (y1 - y3) ** 2
print(CAsqr)

CAx = (x3 + x1) / 2
CAy = (y3 + y1) / 2
plt.text(CAx - 1.3, CAy, f'AC({x1 - x3}, {y1 - y3})', rotation = 65)

#set the xlim and ylim
plt.xlim(-10,15)
plt.ylim(-2,10)

plt.show()

225
164
89
In [15]:
x1, y1 = -5, 0
x2, y2 = 10, 0
x3, y3 = 0, 8

plt.plot(x1, y1, marker = 'o', markersize = 10)
plt.plot(x2, y2, marker = 'o', markersize = 10)
plt.plot(x3, y3, marker = 'o', markersize = 10)

# connecting all three points to make triangle
plt.plot( 
    (x1, x2, x3, x1),   
    (y1, y2, y3, y1)    
)

# name of the points 
plt.text(x1 - 2.3, y1 + 0.3, f'A({x1}, {y1})')
plt.text(x2 + 0.4, y2, f'B({x2}, {y2})')
plt.text(x3, y3 + 0.3, f'C({x3}, {y3})')


# AB distance 
ABsqr = (x2 - x1) ** 2 + (y2 - y1) ** 2
#print(ABsqr)
AB = ABsqr ** 0.5 

ABx = (x1 + x2) / 2
ABy = (y1 + y2) / 2
plt.text(ABx, ABy - 0.6, f'AB({x2 - x1}, {y2 - y1}) = {AB}')

# BC distance
BCsqr = (x3 - x2) ** 2 + (y3 - y2) ** 2
#print(BCsqr)
BC = round(   BCsqr ** 0.5, 2    )

BCx = (x2 + x3) / 2
BCy = (y2 + y3) / 2
plt.text(BCx - 2, BCy - 1, f'BC({x3 - x2}, {y3 - y2}) = {BC}', rotation = -50)

# CA distance
CAsqr = (x1 - x3) ** 2 + (y1 - y3) ** 2
#print(CAsqr)
CA = round(   CAsqr ** 0.5, 2    )

CAx = (x3 + x1) / 2
CAy = (y3 + y1) / 2
plt.text(CAx - 1.3, CAy, f'AC({x1 - x3}, {y1 - y3}) = {CA}', rotation = 65)

#set the xlim and ylim
plt.xlim(-10,15)
plt.ylim(-2,10)

plt.show()
In [ ]:
In [ ]:

kindergarten

  1. Arithmetic
  2. Identify Pictures
  3. Learn Words

Python for kids

  1. How We Teach Exponents and Powers to Kids
  2. Plotting points
  3. Learning shapes, size and color
  4. Learning Coordinate Geometry
  5. Draw Shapes With Points Using Matplotlib Module
  6. Learn Coordinate Geometry With Intuitive Way - Part 1
  7. Teaching Geometry to Grade 3 Kids
  8. Plotting Simple Line, Bar And Pie Chart
  9. Draw Dream House Using Python Matplotlib Module
  10. Draw Circle - Diameter, Radius, Arc and Segment Using Python Matplotlib Module
  11. Draw Badminton Court Using Python Matplotlib Module
  12. Let Us Play With Carrom Board in Python
  13. Draw Some Interesting Pattern With Numpy & Matplotlib Module
  14. Step by Step Draw Boy Using Matplotlib Module
  15. Make Shapes With SystemOfBobies
  16. Draw Cartoon
  17. Draw Two Cartoons Inside House
  18. 3Dimension Plotting in Python
  19. Solar System
  20. Plot World, Continent and Cities
  21. Text Data Handling
  22. Draw Properties of Triangle Using the Python Matplotlib Module

Fourier series

  1. Plotting fourier series

Linear Equations

  1. Linear Equations

Geometry

  1. Cone geometry
  2. Cube geometry
  3. Cylinder geometry
  4. Disk geometry
  5. Open top box geometry
  6. Rectangle geometry
  7. Ring geometry
  8. Saturn geometry
  9. Sphere geometry

Laplace

  1. Laplace transfomation plotting in 3D

Vectors

  1. Reference frames 3d
  2. Vector implimentation 2 vectors
  3. Vector with numpy and sympy

Differential equations

  1. First order differential equations

Functions

  1. Function plotting in 3D
  2. Function plotting in 2D

Jacobian

  1. Jacobian

Lagrangian

  1. Lagrange multipliers
  2. Lagrange example

Waves

  1. Plot electromagnectic waves

Electromagnetism

  1. Field plot
  2. Electric fields
  3. Fields
  4. Charges on Equilateral Triangle

Optics

  1. Lens optics geometry
  2. Mirror optics geometry

Quantum mechanics concepts

  1. Dirac notation and photon polarisation
  2. Photon polarisation
  3. Electron spin
  4. Position momentum and heisenberg
  5. The EPR paradox explanation
  6. Energy operators the hamiltonian and schrodinger
  7. The harmonic oscillator
  8. Schrodinger equation a simple derivation

Theory of relativity

  1. Derivation of time dilation
  2. Gamma factor
  3. Spacetime reference frames equations

Kinematics

  1. Circular motion

Thermodynamics

  1. Entropy and the second law of thermodynamics
  2. Introductory chemical engineering thermodynamics

Formulae

  1. Formulae

A level physics

  1. Classical mechanics

Chemistry

  1. ChemCalcManager
  2. ChemistryFormulaManager
  3. ElementGroupManager
  4. ElementsManager
  5. EnvironmentManager
  6. MolarManager
  7. MoleculesManager
  8. PeriodicTableManager
  9. ReactivityManager
  10. SmilesManager
  11. VisualizationManager

English

  1. Book Manager
  2. Word Manager
  3. Grammar Manager
  4. Tense Manager
  5. Vocabulary Manager
  6. Learn Language Manager
  7. I sat with cat - Poem by Ishwarya
  8. There was a bug - Poem by Ishwarya
  9. The dog was doing a jog - Poem by Ishwarya

Geography

  1. Solar System
  2. Plot World, Continent and Cities

Animation

  1. Animate Circle With SVG
  2. Animate Stars in Different Directions Kids
  3. Move Box in HTML

Plotting

  1. Matplotlib Introduction
  2. Single Line Plots
  3. Bar Plots
  4. Histograms Plots
  5. Types of Plotting
  6. Seaborn Introduction
  7. Seaborn Scatterplot
  8. Seaborn Barplot
  9. Seaborn Boxplot
  10. Seaborn Pairplot
  11. Seaborn Heatmap
  12. Seaborn Seaborn Pandas
  13. Seaborn Plot a Simple Linear Relationship Between Two Variables
  14. Seaborn Displot
  15. Seaborn Palette
  16. Three-Dimensional Plotting in Matplotlib
  17. Interactive Visualizations With Bokeh Part 1
  18. Data Visualization With Seaborn - Part 1
  19. Draw Concrete Jungle In Matplotlib
  20. Draw Beautiful Eyes in Python Using the Matplotlib Module
  21. Celebrate Valentine With Your Partner and Python

SVG

  1. SVG Shapes
  2. SVG Shapes Advanced
  3. Animate Circle With SVG
  4. SVG Animation
  5. SVG Text
  6. Can We Write Alphabets With Help of SVG?

Python

  1. Searching Text in Multiple Files in Python
  2. Working With MongoDB & Python Using PyMongo and Pandas
  3. Capture Date, Phone and Email From Text With Regular Expression in Python
  4. Set Operations in Python
  5. Extract Table Data From Wikipedia Using Web Scraping With Python
  6. Word Cloud for a Website
  7. Sqlite Relational Database Management With Python
  8. How to Import Data From a MySql Database Into Pandas Data Frame
  9. Python Object Serialization and Deserialization With Pickle
  10. Regular Expression Operations in Python
  11. Creating and Writing to Different Type of Files in Python
  12. Convert Word file to PDF, HTML and PDF to JPG, PNG in Python

Machine Learning

  1. Deal Banking Marketing Campaign Dataset With Machine Learning

TensorFlow

  1. Difference Between Scalar, Vector, Matrix and Tensor
  2. TensorFlow Deep Learning Model With IRIS Dataset
  3. Sequence to Sequence Learning With Neural Networks To Perform Number Addition
  4. Image Classification Model MobileNet V2 from TensorFlow Hub
  5. Step by Step Intent Recognition With BERT
  6. Sentiment Analysis for Hotel Reviews With NLTK and Keras
  7. Simple Sequence Prediction With LSTM
  8. Image Classification With ResNet50 Model
  9. Predict Amazon Inc Stock Price with Machine Learning
  10. Predict Diabetes With Machine Learning Algorithms
  11. TensorFlow Build Custom Convolutional Neural Network With MNIST Dataset
  12. Deal Banking Marketing Campaign Dataset With Machine Learning

PySpark

  1. How to Parallelize and Distribute Collection in PySpark
  2. Role of StringIndexer and Pipelines in PySpark ML Feature - Part 1
  3. Role of OneHotEncoder and Pipelines in PySpark ML Feature - Part 2
  4. Feature Transformer VectorAssembler in PySpark ML Feature - Part 3
  5. Logistic Regression in PySpark (ML Feature) with Breast Cancer Data Set

PyTorch

  1. Build the Neural Network with PyTorch
  2. Image Classification with PyTorch
  3. Twitter Sentiment Classification In PyTorch
  4. Training an Image Classifier in Pytorch

Natural Language Processing

  1. Spelling Correction Of The Text Data In Natural Language Processing
  2. Handling Text For Machine Learning
  3. Extracting Text From PDF File in Python Using PyPDF2
  4. How to Collect Data Using Twitter API V2 For Natural Language Processing
  5. Converting Text to Features in Natural Language Processing
  6. Extract A Noun Phrase For A Sentence In Natural Language Processing

Others

  1. test-nutan
  2. QuestionManager.ipynb
  3. ActivityManager.ipynb
  4. Why us?
  5. How to Setup Wordpress Website Step by Step in Ubuntu VPS
  6. Setup Plesk Panel and Deploy Wordpress Website in Ubuntu VPS - Part 1
  7. Deploy a New Server With Plesk Control Panel - Part 2
  8. Setup Plesk Control Panel For Wordpress Website - Part 3
  9. Deploy Wordpress Website In Plesk Control Panel - Part 4
  10. HTML Basic Example
  11. Install MongoDB Community Server in Windows10
  12. How to Setup SAP BTP Trial Account and Create SAP HANA Cloud Database
  13. Connect SAP Hana Cloud Database Through Python
  14. How To Create a Self-Signed SSL Certificate for Apache in Ubuntu Virtual Cloud Server
  15. Consume Rest API in Django Web Application
  16. Setup GIT Repository in Ubuntu VPS
▲